Formació d'imatges


Lleis fonamentals de les trajectòries lluminoses
Per tal d'entendre el funcionament de diferents elements com els miralls, els diòptrics o les lents a l'hora de formar imatges hem de tenir en compte les lleis següents:
-
La llum es propaga en línia recta quan va per un material transparent i homogeni.
-
Conservació del pla d’incidència en la reflexió i la refracció. El pla d’incidència està definit pel raig incident i la normal en el punt d’incidència. Els rajos reflectits i refractats estan continguts en aquest mateix pla.
-
Les trajectòries de la llum són reversibles. Això implica que si per anar d’un punt A a un altre B, la llum ha seguit una trajectòria T; per anar del punt B al A, seguirà la mateixa trajectòria T.

REFRACCIÓ DE LA LLUM


Formació d'imatges
 |  |  |
|---|---|---|
 |  |  |
 |  |  |
Considerem un punt emissor de llum O. Quan els rajos que passen per O es reflecteixen o es refracten en una o vàries superfícies òptiques, es reuneixen en un punt O’, la imatge de O.
Aquesta imatge pot ser real, si els rajos de veritat es tallen en aquest punt, o virtual si són les prolongacions dels rajos les que es tallen. A la pràctica, una imatge real és aquella que es pot recollir en una pantalla, mentre que una imatge virtual no, tot i que es pugui veure com a real. Un exemple d’imatge virtual és la que es forma en un mirall pla.
Si ens fixem en altres criteris, una imatge pot ser dreta o invertida segons la seva orientació respecte a l’objecte que representa, i pot ser una imatge major, menor o igual respecte a la mida de l'objecte.
MIRALL PLA
La imatge que es forma amb qualsevol mirall pla d’un objecte real té les següents característiques:
-
És virtual
-
Té la mateixa mida que l’objecte
-
Es troba a la mateixa distància del pla del mirall que l’objecte
-
És simètrica respecte a l’objecte

DIÒPTRIC PLA
Tots els rajos que surten d’un punt objecte i travessen una superfície plana refractant (o diòptric) no es tornen a ajuntar en un únic punt imatge i, en conseqüència, la posició de la imatge és diferent segons la inclinació del feix de rajos que arriba a l’observador.

Per exemple, en aquesta imatge la profunditat aparent, que és la posició de la imatge respecte de la superfície de l’aigua, és menor que la profunditat real a la que es troba l’objecte i va disminuint conforme els rajos emergents que arriben a l’observador són més inclinats (posició P2 del observador respecta a les posicions P1 i V).
La posició aparent de la imatge S’ a partir de l’expressió on n i n’ són els índex de refracció del primer i el segon medi, respectivament, i S és la posició real de l’objecte respecte a la superfície. La imatge a través de la superfície plana refractant té la mateixa mida que l’objecte.
MIRALL ESFÈRIC
Un mirall esfèric és una superfície reflectant amb forma de casquet esfèric. L’eix òptic uneix el centre de curvatura del mirall amb un punt de la seva superfície o vèrtex. La posició de la imatge que es forma amb un mirall esfèric, S’, es pot calcular mitjançant l’expressió , on S i S’ són les distàncies entre el vèrtex del mirall i l’objecte, i el vèrtex i la imatge, respectivament, i R és el radi. En un mirall esfèric, els augments (relació entre la mida de la imatge i la del objecte) valen , on Y és la mida de l’objecte i Y’ la de la imatge, i m els augments.


Un objecte que es troba molt llunyà del mirall (S = - ) sobre la direcció de l’eix òptic forma una imatge sobre el focus del mirall (F), un punt la posició del qual ve donada per la distància focal del mirall (f = R/2). És a dir, quan un raig arriba paral·lel a l'eix, en reflectir -se passarà per el focus del mirall i, al contrari, si un raig incideix sobre el mirall passant pel focus es reflectirà paral·lel a l’eix òptic. Si un raig incideix en la direcció del radi (el raig passa pel centre de curvatura), es reflectirà sobre la mateixa direcció, però en sentit contrari. El raig incident que apunta al vèrtex del mirall es reflexa seguint una trajectòria paral·lela a l’eix òptic.
Un mirall esfèric pot ser còncau o convex, depenent de la seva curvatura en relació amb la llum incident.
Mirall convex
Mirall còncau
Un mirall convex té un radi positiu i, generalment, les imatges que forma d’un objecte real són virtuals, dretes i de menor mida. És un tipus de mirall que permet l'observació d’un camp objecte molt extens, per això és utilitzat en sistemes de seguretat, per millorar la visibilitat en creuaments, en els retrovisors, etc.
Un mirall còncau té un radi negatiu i, al contrari dels miralls convexos, la imatge que forma d’un objecte real depèn en gran mesura de la posició de l’objecte. A continuació tenim les cinc configuracions més destacades o de més interès:
-
Quan l’objecte està més lluny del centre de curvatura, la imatge és real, invertida i menor.
-
Quan l’objecte està en el centre, la imatge que es forma és real, invertida i d’igual mida.
-
Quan l’objecte es troba entre el centre i el focus del mirall, la imatge és real, invertida i major que l’objecte.
-
Quan l’objecte es col·loca en el focus no es forma imatge.
-
Quan l’objecte està entre el focus i el vèrtex del mirall, la imatge que es forma és virtual, dreta i major que l’objecte.

DIÒPTRIC ESFÈRIC
Un diòptric esfèric és una superfície en la qual es produeix reflexió de la llum i que té simetria esfèrica. L’eix òptic uneix el centre de curvatura del diòptric amb un punt de la seva superfície o vèrtex. La posició de la imatge que es forma a través d’un diòptric esfèric, S’, es pot calcular mitjançant l’expressió , on S i S’ són la distància des del vèrtex del diòptric a l’objecte i a la imatge respectivament; n és l’índex de refracció del medi per el qual incideix la llum; n’ és l’índex de refracció del medi pel qual emergeix la llum refractada, y R és el radi.
En un diòptric esfèric, els augments m es defineixen com: .

Els rajos que incideixen en el diòptric paral·lels a l’eix, al refractar-se, passen pel focus imatge F’ del diòptric, que és un punt la posició del qual ve marcada per la distància focal imatge f’ mesurada des del vèrtex: . Els rajos que incideixen en el diòptric passant pel focus objecte F, després de la refracció emergeixen paral·lels a l’eix. I els rajos que passen pel centre de curvatura no es desvien al travessar la superfície del diòptric.

Les característiques d’una imatge poden ser molt variades i depenen de: els índex de refracció dels materials anterior i posterior, el radi de curvatura, l'orientació còncava o convexa de la curvatura, y la posició de l’objecte respecte al vèrtex del diòptric.
Aquí tenim alguns exemples de imatges ques es formen a través de diòptrics esfèrics:
-
A l'esquerra, a la peixera, la imatge és augmentada i dreta.
-
A la dreta, a les gotes d'aigua, la imatge és invertida i menor


LENTS
Les lents es consideren un sistema òptic format per la unió de dos diòptrics, generalment esfèrics, i que separen dos medis amb índexs de refracció diferents als de la lent. Aquest sistema denominat lent es caracteritza per el seu índex de refracció, pels seus radis de curvatura i per els índex de refracció dels medis externs que separa, que solen ser iguals. La línia que uneix els dos diòptrics s’anomena «eix òptic de la lent».
La fabricació d’aquestes lents remunta segles enrere i el seu ús està molt generalitzat avui en dia, sobretot en la correcció de problemes visuals amb les ulleres i les lents de contacte, però també són utilitzades en diferents instruments òptics com poden ser els microscopis, els telescopis o les càmeres fotogràfiques entre altres.
En general, el gruix (g) de les lents sol ser molt petit en comparació amb els seus radis de curvatura i les distàncies objecte i imatge, és per això que es pot considerar inapreciable, denominant-les en conseqüència «lents primes». En aquestes circumstàncies, la distància objecte al segon diòptric serà igual a la distància imatge del primer (és a dir: S2=S’1-g ≈S’1). Amb aquestes aproximacions, els vèrtex de les dues superfícies (V1 i V2) poden considerar-se coincidents en un únic punt denominat «centre òptic de la lent».

Tenint en compte les característiques anteriors i a partir de la suma de les equacions dels diòptrics (ja vistes en l’apartat anterior) que forma una lent, arribem a l’equació de les lents:

(si considerem que l’índex de refracció del medi exterior és 1, aire)
També és interessant veure com en una lent prima, quan li arriben rajos procedents d’un punt llunyà (S= ), la imatge es forma en un punt anomenat focus imatge (F’), que es troba a una distància f’ del vèrtex de la lent. I al contrari, quan a una lent li arriben rajos procedents d’un punt que es troba a una distància f, el focus objecte (F), formen la imatge a l’infinit (S’= ). Amb tot això i a partir de l’equació de les lents deduïm: i i que per tant f’ = -f .
La potència d’una lent, P, indica la capacitat que té la lent per fer convergir o divergir els raigs de llum incidents. La potència es defineix com la inversa de la distància focal (f): . La unitat de la potència és la diòptria, D, quan la distància focal, f, està en metres. La potència d’una lent convergent és positiva, mentre que la potència d’una lent divergent és negativa. Això es deu a que la distància focal (f) de les lents convergents és positiva mentre que la de les lents divergents és negativa.

Tenint en compte tot el que hem vist, ara anem a veure com serà la imatge que es formarà d’un objecte a través d’una lent prima (de la qual coneixem el focus).
Per poder fer això, utilitzarem rajos dels quals la trajectòria sigui coneguda:

-
Els rajos que incideixen a la lent paral·lels a l’eix, al refractar-se, passen pel focus imatge F’ de la lent.
-
Els rajos que incideixen a la lent passant pel focus objecte F, després de la refracció emergeixen paral·lels a l’eix.
-
I els rajos que passen pel centre de la lent no es desvien al travessar la superfície de la lent.
Existeixen dos tipus de lents formades a partir de dos diòptrics esfèrics:
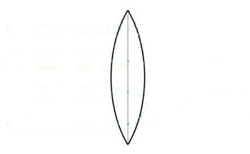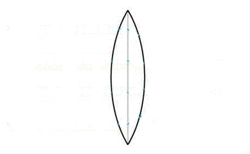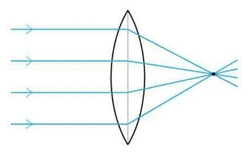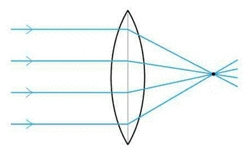
Lent convergent
S’anomenen lents convergents aquelles que tenen una focal positiva i els rajos procedents de l’infinit, al incidir sobre la lent, convergeixen cap al punt F’.
Les imatges que es formen a través d’una lent convergent són molt variades i depenen en gran mesura de la posició de l’objecte. A continuació tenim les cinc configuracions més destacades o de més interès:
-
Quan l’objecte està més lluny del doble de la distància del focus, 2F, la imatge és real, invertida i menor.
-
Quan l’objecte es troba al doble de la distància focal, 2F, la imatge és real, invertida i d’igual mida.
-
Quan l’objecte es col·loca entre el doble de la focal i el focus, la imatge que es forma és real, invertida i major.
-
Quan l’objecte està al focus, F, no es forma imatge.
-
Quan l’objecte es troba entre el focus i la lent, la imatge és virtual, dreta i major.

Lent divergent
Pel contrari, les lents divergents són aquelles que, quan hi incideixen rajos procedents de l’infinit, emergeixen divergents i són les seves prolongacions les que es concentren en F’, que ara serà virtual.
Les imatges que es formen a través d’una lent divergent tenen sempre les mateixes característiques: virtuals, dretes i menors.






